さて、前の記事で紹介した自動翻字のアルゴリズムについて、少し中身を覗いてみましょう。

論文では、隠れマルコフモデル（HMM）、最大エントロピーマルコフモデル（MEMM)、双方向長短期記憶（BiLSTM)ニューラルネットワークの３つのモデルを使って翻字変換を行い、それぞれの精度を比較しています。

すごーく簡単にこれらのモデルの違いを説明すると、HMMは一つ前の文字との、MEMMでは前後二つずつの文字との関係性から翻字を推測しています。またMEMMでは翻字が限定符かどうかなど文脈情報も学習に取り入れています。BiLSTMでは文章全体から判断しています。いずれも自然言語処理や音声認識の分野でよく使われる手法です。

	HMM	MEMM	BiLSTM
翻字と分割	89.5%	94%	96.7%
翻字のみ	93.6%	96.4%	97.8%
分割のみ	91.8%	95.9%	97.9%

それぞれの手法の精度は上記の通りとのことでした。これはひとつのコーパス（RINAP)から80%の文を学習に、10%を検証に、10%を評価に使ったものです。HMMよりもMEMMの方が、MEMMよりもBiLSTMのほうが精度が高いのはひとつの文字の読みを決定するのに使う情報が後者の方がより多いことからも納得のいくものです。

今回は、公開されているコードとデータを元に、HMMでの翻字推測の手法について見ていきましょう。

例として、前の記事で挙げた文から最初の5文字𒂊𒉡𒈠𒀭𒈨𒌍 e-nu-ma DINGIR.MEŠを見てみましょう。文字としては5文字ですが、ユニコードの符号としては6つあります。まずは、各符号ごとにどのような読み方の候補があるのかをAkkademiaのデータから見てみましょう。

𒂊	𒉡	𒈠	𒀭	𒈨	𒌍
e- 2444	nu 2442	ma 4258	{d}- 3956	MEŠ(0) 4927	MEŠ(1) 4927
e 1231	nu- 1354	ma- 2049	DINGIR. 1076	MEŠ(0)- 1886	MEŠ(1)- 1886
E 12	NU 17	MA 378	AN. 1001	me- 984	30- 239
PA₅(1) 4	NU. 8	MA. 23	an- 735	me 855	30 235
E. 3	nu. 4	PEŠ₃ 1	an 387	ME 327	eš- 208
		MA- 1	DINGIR 239	šib 199	meš(1) 121
			DINGIR- 141	mi₃- 155	iš₃ 35
			AN- 107	meš(0) 121	sin- 28
			AM₃(1) 42	šip- 91	34(0) 21
			AN 37	šib- 89	EŠ. 19
			ŠEG₃(1). 17	mi₃ 29	eš 19
			il₃ 15	meš(0)- 18	meš(1)- 18
			el₃ 4	ABGAL(1) 18	95(1) 10
			diŋir- 3	ME- 14	30. 7
			GARZA(1). 3	šep- 8	90(1) 6
			NIDBA(1). 3	sib 7	33(0) 4
			il₃- 2	ME. 7	32(0) 4
			diŋir 2	šeb- 3	sin 3
			NIDBA(1) 1	sip- 3	31(0) 3
			ŠEG₃(1) 1	sib- 2	39(0) 3
					ba₃- 1
					EŠ 1
					91(1) 1
					35(0) 1
					99(1) 1
					ṣin- 1
					30+ 1

Akkademiaではeとe-のように、そこで単語が終わるものと、次に続く文字があるものをわけて分類しているようです。ひとつのモデルで翻字の変換と単語のセグメンテーションを同時に表現しようとしているわけですね。同様にeとEのようにアッカド語の単語の一部の場合とシュメール語の単語の一部の場合もわけています。またPA₅(1)とあるのは、2つのユニコード符号𒉽𒂊で表現されるPA₅という文字を、𒉽をPA₅(0)、𒂊をPA₅(1)としているわけです。{d}のように波括弧で囲まれているのは限定符を表現しています。符号の横の数字はコーパス中の発生頻度です。

符号ごとに最も発生頻度の高い読みを選んで並べてみるとこうなります。

e-nu ma {d}-MEŠ(0)MEŠ(1) = e-nu ma ^dMEŠ

この時点でだいぶ正解に近いですね。このように1文字、あるいは1単語ごとにデータを区切ったものをユニグラムといいます。対して、隣接する2文字を1文字ずつずらしながら区切ったものをバイグラムといいます。今回のHMMモデルでは2文字のバイグラムを使っています。この例では下記のようにバイグラムごとにコーパス中の発生頻度を調べます。

𒂊𒉡	𒉡𒈠	𒈠𒀭	𒀭𒈨	𒈨𒌍
e-nu 45	nu-ma 75	ma {d}- 32	DINGIR.MEŠ 722	MEŠ 4927
e-nu- 43	nu ma- 12	ma-an- 32	DINGIR.MEŠ- 81	MEŠ- 1886
e nu- 4		ma an- 7	DINGIR.ME 24	meš 121
		ma-an 6	MEŠ- 11	meš- 18
		ma AN. 5	an-me- 7	ME 30 5
		ma DINGIR. 5	MEŠ 6	ME 34 4
			MEŠ 3	ME 30. 3
			AN ME 1	me-eš 1
				ME 30+ 1
				me eš- 1

​ ユニグラムの表よりも随分コンパクトになりましたね。𒂊も𒉡もそれぞれ5種類の翻字表現があったわけですが、𒂊𒉡という並びではコーパス全体でもe-nu e-nu- e nu-の3つの組み合わせでしか使われていなかったことがわかります。

またe-nuのようにここで単語が区切られる場合とe-nu-のようにあとに文字が続く場合はだいたい同じ頻度ですが、nu-maとnu ma-ではだいぶ開きがあることもわかりました。この3文字をつなげた𒂊𒉡𒈠で考えると、e-nu ma-よりもe-nu-maと読むほうが確率が高そうだと予想できます。

それぞれのバイグラムのつながりを図示したものがこちらです。

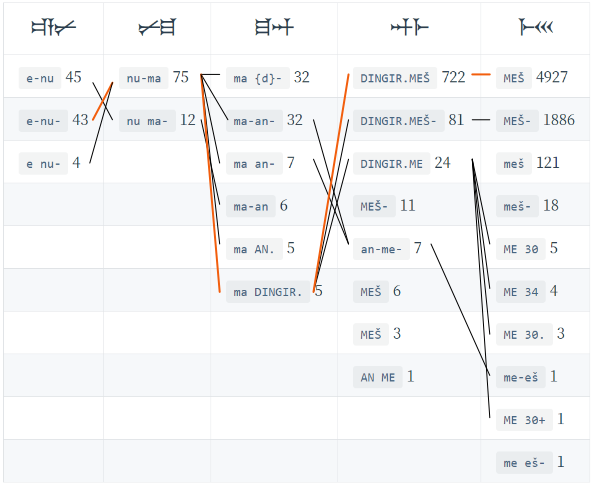
こうしてみると、先頭から最後までつながるルートはずいぶん限られていることがわかります。正解のルートをオレンジの線で図示してみました。

ただ、つながりだけを考えるとe-nu ma-an-me-ešというルートもありますね。

このようなバイグラムごとの発生頻度からもっとも可能性の高いルートを効率よく発見する手法として、ビタビアルゴリズム (opens new window)というものが知られており、広く使われています。その詳細にはここでは踏み入れませんが、実装が比較的簡単で計算量も程よい、とってもよいアルゴリズムです。

このデータにビタビアルゴリズムを適用すると、果たしてe-nu-ma DINGIR.MEŠという結果が得られます。たった2文字だけの関連性だけを見ているわけですが、これでもまあまあの結果は得られることは示せたでしょうか。なお、隠れマルコフモデル（HMM）はバイグラムでしか使えないわけではなく、任意のnグラムに拡張できるのですが、nが大きくなるほどコーパス中の出現頻度が小さくなってしまいます。コーパスに出現しない並びに対しては発生確率を計算できないため、楔形文字文書のように入手できるコーパスの大きさに制限がある環境では限界があるといえますね。

またHMMに限らないのですが、このような手法ではコーパスに存在しない並びの文字に対して無力です。たとえば𒌍はバビロニア数字の30でもあるのでバイグラムにもME 30とかME 34という読みが登場します。数字であればこの他にも35でも37でもいいはずですが、この手法ではコーパスに登場する数字しか認識できないのですね。数字については別途トークン化するような処理が必要そうです。

今回は論文に使われている3つの手法のうち隠れマルコフモデル（HMM）について紹介しました。最大エントロピーマルコフモデル（MEMM）や双方向長短期記憶（BiLSTM)ニューラルネットワークについてはよく知らないのでこんな風には説明できないのですが、なにか面白いことがわかるかどうか少しコードで遊んでみるつもりです。